如何构建一个神经网络

人工神经元（Artificial Neuron）

• 每一个神经元都是一个非常简单的线性函数。在激活函数之前，先对上一层的每个神经元的数据进行一个加权的运算。

$$z(x) = \sum_i w_ix_i +b= w^Tx+b$$

• 但是只有线性运算显然是不够的，因为无论涉及再多层的线性运算最终都可以等价成一层线性运算，因此在每一层中间还需要设计一个激活函数 $a(x)$ 。

$$a(x)=f(z(x))= f(w^Tx+b)$$

• 其中 $f(x)$ 是一个非线性函数，$w$ 对应每一个上一层的神经元的权重(weight)，而 $b$ 代表上一层的偏差(bias)。

激活函数和饱和

激活函数

常见的激活函数有：Linear、Sigmoid、Hyperbolic tangent、Rectified linear、Softmax。

Linear activation function

• 线性激活函数一般不用于深度学习的神经网络中，原因就是它并没有做非线性的变化，导致再多层的线性变化都等价于一层。

$$f(z):=z$$

• 但是激活函数如果采用非线性函数，就可以通过设计多层的结构让函数变得更加复杂，能够完成更加精确的近似。

Sigmoid activation function

• Sigmoid函数可以将神经元的输出压缩到 $(0,1)$ 之间，并且是一个严格单调递增的有界函数，在分类应用中用途十分广泛。

$$f(z):= \frac{1}{1+e^{-z}}$$

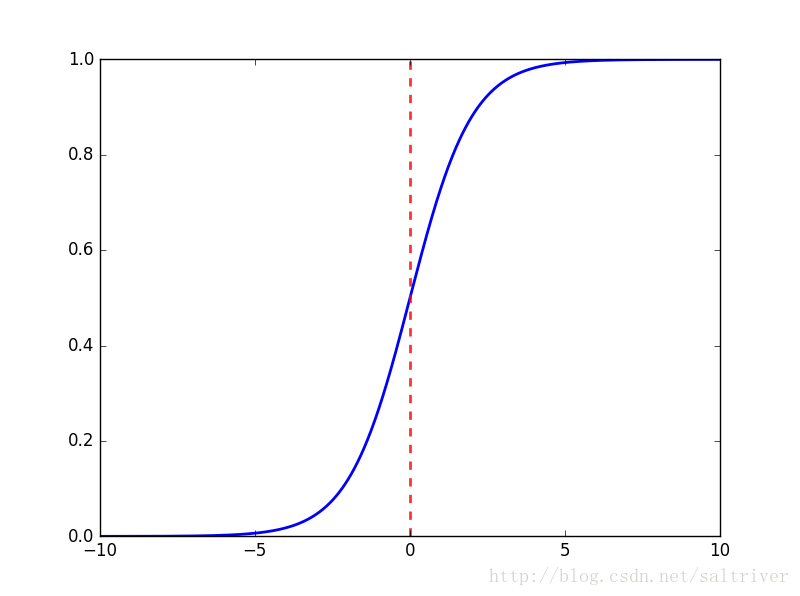
Hyperbolic tangent(tanh) activation function

• Tanh函数可以将神经元的输出压缩到 $(-1,1)$ 之间，使得输出结果可正可负，并且也是一个严格单调递增的有界函数。

$$f(z):=\frac{\exp (2z)-1}{\exp (2z) +1}$$

Rectified linear (ReLU) activation function

• ReLu又叫做修正线性单元，在最近的深度学习网络中也十分常用。主要优势有：它在SGD中收敛速度要比Sigmoid和tanh快很多；可以解决梯度消失的问题；对神经网络可以使用稀疏表达等。

$$f(z):= max(0,z)$$

• ReLu还有很多变体：

  • Shift ReLU：$f(z):=max(1,z)$

  • Leaky ReLU: $f(z):= max(0.1z,z)$

  • Parameter ReLU: $f(z):=max(\mu z, z)$

  • Exponential Linear Units: $f(z):=max(z,\mu(\exp(z)-1))$

Softmax activation function

• Softmax叫做归一化指数函数，是逻辑函数的一种推广。它能将一个含任意实数的K维向量压缩到另一个K维向量中，且保证每个元素的范围都在 $(0,1)$ 之间，并且总和为1。压缩以后的每一个元素值为：

$$\sigma(z_j)= \frac{\exp(z_j)}{\sum_c \exp(z_c)}$$

• 经过压缩以后得到的向量为：

$$f(z)=Softmax(z)=[\frac{\exp(z_1)}{\sum_c \exp(z_c)},\cdots,\frac{\exp(z_c)}{\sum_c \exp(z_c)}]^T$$

激活函数的特征

• 连续可导（允许少数点上不可导）的非线性函数。

• 激活函数及其导函数要尽可能简单，有利于网络计算效率。

• 激活函数的导函数的值域要在一个合适的区间内，太大或者太小都将影响训练的效率和稳定性。

饱和（saturation）

• 右饱和：当x趋向于正无穷时，函数的导数趋近于0，此时称为右饱和。

• 左饱和：当x趋向于负无穷时，函数的导数趋近于0，此时称为左饱和。

• 饱和函数与非饱和函数：当一个函数既满足右饱和，又满足左饱和，则称为饱和函数，否则称为非饱和函数。

• 常用的饱和激活函数有Sigmoid和tanh，非饱和函数有ReLU；相对于饱和函数而言，非饱和函数可以解决梯度消失的问题，加快收敛速度。

前馈神经网络

原理

• 前馈神经网络采用一种单向多层结构。其中每一层包含若干个神经元。

• 在此种神经网络中，各神经元可以接收前一层神经元的信号，并产生输出到下一层。

• 第0层叫输入层，最后一层叫输出层，其他中间层叫做隐含层（或隐藏层、隐层）。隐层可以是一层，也可以是多层。

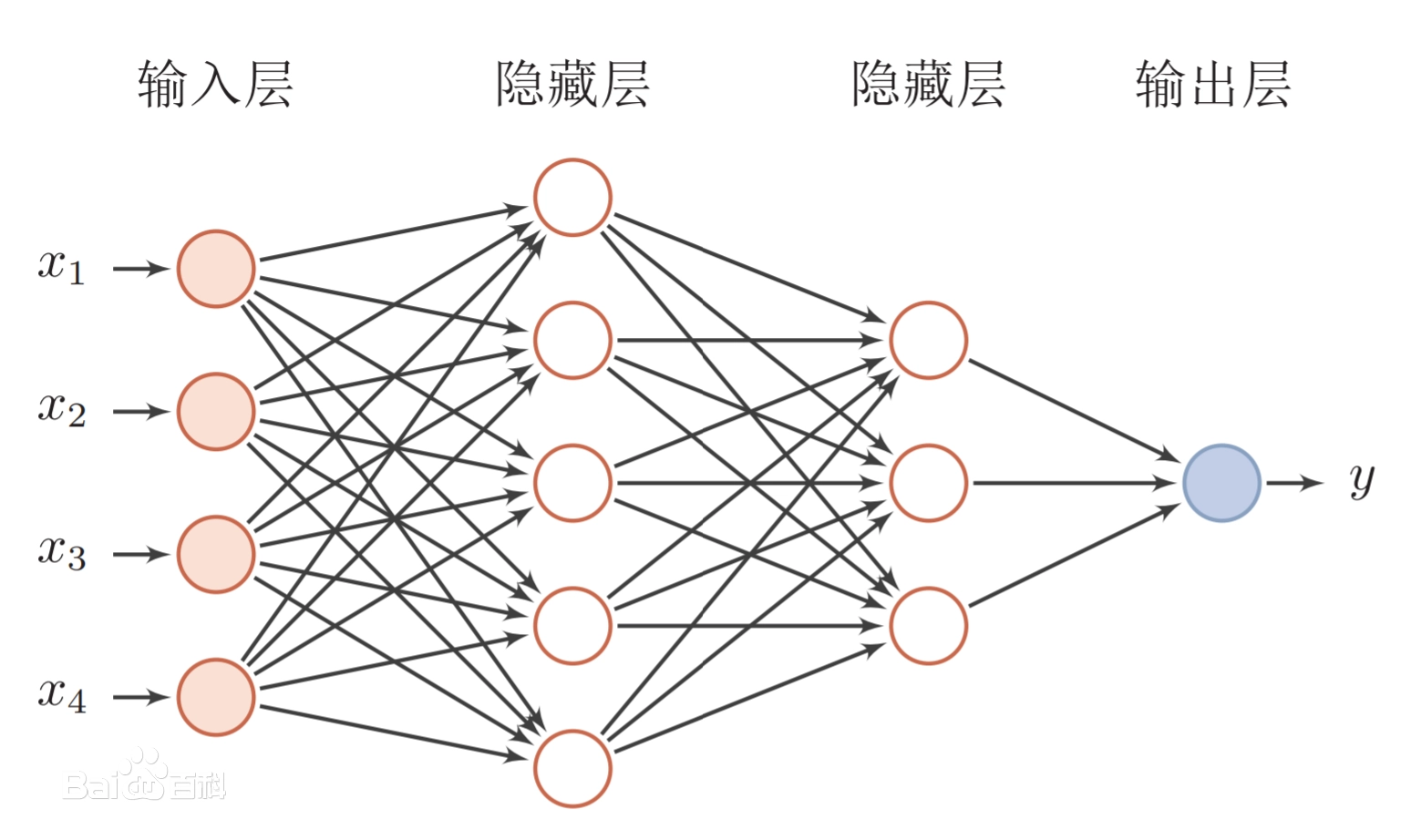
• 模型的层数越多或者每一层模型中的神经元越多，模型能够表达的函数就越多，能够近似更加复杂的函数。

• 全连接前馈神经网络：顾名思义，就是神经网络中的每一层里的所有神经元都和下一层的所有神经连接。

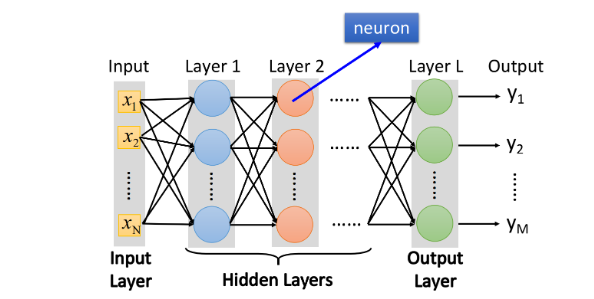
符号说明

假设总共有 $m$ 层隐藏层，其中第 $l-1$ 层有 $p$ 个神经元，第 $l$ 层有 $q$ 个神经元。

• $a_i^l$ ：表示第 $l$ 层的第 $i$ 个神经元经过激活函数后的输出。

• $a^l$ ：表示第 $l$ 层的所有神经元的输出，是一个 $q \times 1$ 的向量。

• $z_i^l$ ：表示第 $l$ 层第 $i$ 个神经元激活函数的输入（线性函数的输出）。

• $z^l$ ： 表示第 $l$ 层激活函数的输出，是一个 $q\times 1$ 的向量。

• $w^l_{i,j}$：表示第 $l-1$ 层的第 $i$ 个神经元到第 $l$ 层第 $j$ 个神经元的权重。

• $W^l$ ：表示第 $l-1$ 层神经元到第 $l$ 层神经元的权重矩阵，是一个 $p\times q$ 的矩阵。

• $b_i^l$ ：表示第 $l$ 层的第 $i$ 个神经元的偏置。

• $b^l$ ：表示第 $l$ 层的偏置，是一个 $q\times 1$ 的向量。

全连接前馈神经网络函数推导

• 输入是一个 $N$ 维向量，输出是一个 $M$ 维向量，激活函数是 $\sigma(x)$。

• 因此输出层 $y$ 等价于：

• 或者写作：

如何训练一个神经网络

从宏观上来讲，训练一个神经网络（模型）的过程大致分为两部分。第一，构建损失函数。第二，优化损失函数。

构建损失函数

• 损失函数可以看做我们需要优化的目标。可以有很多构建损失函数的方法，这一般取决于模型的分布。

• 有时候我们构建的损失函数中还需要加入正则项，来对我们的参数进行一定的惩罚，最终的损失函数都可以等价为：

$$J(\theta) = loss(\hat y -y)+\lambda \Omega(\theta)$$

• 其中 $\Omega(\theta)$ 是正则项，$\lambda$ 是用来衡量正则项的力度。

• 常用的损失函数 $loss()$ 一般有：

  • Square loss: $loss(\hat y,y)=(\hat y-y)^2$

  • Hinge loss: $loss(\hat y,y)=max(0,1-\hat y y)$

  • Logistic loss: $loss(\hat y,y)=\log(1+\exp(-\hat y y))$

  • Cross entropy loss: $loss(\hat y,y)=-y\log\hat y-(1-y)\log(1-\hat y)$

注意 Logistic loss 和 Logistic回归中的损失函数是两回事。 Logistic回归中使用的损失函数是 Cross entropy loss。

优化

损失函数构建完以后，接下来的目标就是对损失函数做优化，找到参数 $\theta$ 使其达到最小值。

GD（梯度下降）

基础知识

• 所谓梯度下降法，就是找到当前所在点下降速度最快的方向（即梯度方向），然后根据这个方向走一定的距离（也叫做学习率/Learning rate），作为下一次迭代的点，以此类推。

神经网络中的GD

• 考虑最简单的神经网络，即不存在任何隐藏层，只有输入和输出层。使用的损失函数为 Cross entropy loss，激活函数为 sigmoid。

• 注意这里是用 $J(\theta)$ ，也就是损失函数对 $w$ 和 $b$ 求导，具体过程如下：

$$J(\theta) = loss(\hat y-y) = y\log\hat y+(1-y)\log(1-\hat y)$$

$$\frac{\partial J(\theta)}{\partial W}=\frac{\partial J(\theta)}{\partial \widehat{y}} \cdot \frac{\partial \widehat{y}}{\partial\left(W^{T} x+b\right)} \cdot \frac{\partial\left(W^{T} x+b\right)}{\partial W}\\[2ex]\frac{\partial J(\theta)}{\partial \hat{y}}=\frac{\partial(y \log \widehat{y}+(1-y) \log (1-\widehat{y}))}{\partial \widehat{y}}=\frac{y}{\widehat{y}}+\frac{y-1}{1-\widehat{y}}\\[2ex]\because \widehat{y}=\frac{1}{1+e^{-\left(W^{T} x+b\right)}}=\frac{1}{1+e^{-z}}\\[2ex]\therefore a^{\prime}(z)=\frac{e^{-z}}{\left(1+e^{-z}\right)^{2}}=\frac{e^{-z}}{1+e^{-z}} \cdot \frac{1}{1+e^{-z}}=(1-\widehat{y}) \cdot \widehat{y}\\[2ex]\therefore \frac{\partial \widehat{y}}{\partial\left(W^{T} x+b\right)}=\frac{\partial a(z)}{\partial z}=a^{\prime}(z)=(1-\widehat{y}) \cdot \widehat{y}\\[2ex]\therefore \frac{\partial J(\theta)}{\partial W}=\left(\frac{y}{\widehat{y}}+\frac{y-1}{1-\widehat{y}}\right) \cdot(1-\widehat{y}) \cdot \widehat{y} \cdot x=(y-\widehat{y}) \cdot x$$

• 当然如果把损失函数换成 Square loss，求导过程也是类似的：

$$J(\theta)=(y-\widehat{y})^{2}\\[2ex]\frac{\partial J(\theta)}{\partial W}=\frac{\partial J(\theta)}{\partial \widehat{y}} \cdot \frac{\partial \widehat{y}}{\partial\left(W^{T} x+b\right)} \cdot \frac{\partial\left(W^{T} x+b\right)}{\partial W}\\[2ex]\frac{\partial J(\theta)}{\partial \widehat{y}}=-2(y-\widehat{y})=2(\widehat{y}-y)\\[2ex]\because \widehat{y}=\frac{1}{1+e^{-\left(W^{T} x+b\right)}}=\frac{1}{1+e^{-z}}\\[2ex]\therefore a^{\prime}(z)=\frac{e^{-z}}{\left(1+e^{-z}\right)^{2}}=\frac{e^{-z}}{1+e^{-z}} \cdot \frac{1}{1+e^{-z}}=(1-\widehat{y}) \cdot \widehat{y}\\[2ex]\therefore \frac{\partial \widehat{y}}{\partial\left(W^{T} x+b\right)}=\frac{\partial a(z)}{\partial z}=a^{\prime}(z)=(1-\widehat{y}) \cdot \widehat{y}\\[2ex]\therefore \frac{\partial J(\theta)}{\partial W}=2(\widehat{y}-y) \cdot(1-\widehat{y}) \cdot \widehat{y} \cdot x$$

• 对 $b$ 求导和对 $w$ 求导唯一的差别在于最后一个偏导，所以只需要在对 $w$ 求偏导的结果中把 $x$ 去掉，结果就是对 $b$ 的偏导。

常用的激活函数及其导数和问题

Sigmoid

• Sigmoid 是曾经最流行的激活函数，函数形式及其导数为：

$$f(z)= \frac{1}{1+\exp(-z)}\ , f'(z)=f(z)\cdot(1-f(z))$$

• Sigmoid函数存在的三个问题：

  • Sigmoid函数在它定义域内的大多数区域都是饱和的，其导数在 $z$ 趋向于正无穷大或者趋向于负无穷大的地方都趋于0。

  • Sigmoid的输出不是0均值的（not zero-center)，导致其在梯度下降的优化变得困难。

  • Exp指数函数要求的算力比较高，不方便计算机计算。

• Sigmoid激活函数在前馈神经网络中不再流行，而是比较广泛地使用于RNN（循环神经网络）、概率模型或者自动化编码等领域。

Tanh

• Tanh激活函数在前馈神经网络中的使用频率高于Sigmoid函数，函数形式及其导数为：

$$f(z)=\frac{\exp (2z)-1}{\exp (2z) +1}\ ,f'(z)=1-f(z)^2$$

• Tanh函数的优点：

  • 在 $z$ 比较小的时候，Tanh函数趋向于线性函数。

  • 输出是0均值的（zero-center)，因此在前馈神经网络的表现优于Sigmoid函数。

• Tanh函数的缺点：

  • 同样存在饱和问题，其导数在 $z$ 趋向于正无穷大或者趋向于负无穷大的地方都趋于0。

  • Exp指数函数要求的算力比较高，不方便计算机计算。

ReLu

• ReLU比较适合用于后向传播，函数形式及其导数为：

$$f(z)=\max(0,z)\ \ ,f'(z)=\begin{cases}1,z\geq 0\\0,0.w.\end{cases}$$

• ReLU的优点：

  • ReLu的收敛速度比Sigmoid和Tanh快。（梯度不会饱和，解决了梯度消失问题）

  • 计算复杂度低，不需要进行指数运算（一般速度在6倍以上）。

• ReLU的缺点：

  • 在 $z=0$ 处不可导，但是实际训练中影响不大。

  • 输出不是0均值的，会影响梯度下降的优化。

  • ReLU不会做幅度压缩，导致数据的幅度会随着模型层数的增加不断扩张。

  • Dead ReLU Problem（神经元坏死现象）：某些神经元可能永远不会被激活，导致相应参数永远不会被更新（在负数部分，梯度为0）。产生这种现象的两个原因：参数初始化问题；学习率太高导致在训练过程中参数更新太大。

• 针对神经元坏死的解决方法：

  • 采用Xavier初始化方法，以及避免将学习率置太大。

  • 使用adagrad等自动调节学习率的算法。

Leaky ReLU

• Leaky ReLU是传统ReLU的变体，函数形式及其导数为：

$$f(z)=\max (0.1 z, z), f^{\prime}(z)=\left\{\begin{array}{l}1, z \geq 0 \\ 0.1,0 . w\end{array}\right.$$

• Leaky ReLU解决了传统ReLU神经元坏死的问题。当然也可以将 $0.1$ 改为 $\mu$，升级成为Parametric ReLU，并且在训练的过程中更新 $\mu$ 的值。

ELU

• Exponential Linear Unit（ELU）也是ReLU的一种变体，函数形式及其导数为：

$$f(z)=\left\{\begin{array}{l}z, z \geq 0 \\ \mu\left(e^{z}-1\right), o . w .\end{array} \quad f^{\prime}(z)=\left\{\begin{array}{l}1, z \geq 0 \\ \mu e^{z}, o . w\end{array}\right.\right.$$

• ELU具有ReLU的所有优点，并且是接近0均值的。

• 美中不足的是ELU需要进行指数运算，对算力要求比较高。

Maxout

• Maxout其实就是一个神经元同时有多个激活函数，全部算一遍以后再取最大的那个。

• Maxout函数的泛化能力比较强，缺点是会导致神经网络的参数成倍增加。

Softmax

• Softmax函数一般用于多分类的问题，而Sigmoid函数用于二分类的问题。

• Softmanx经过压缩后的向量为：

$$f(z)=Softmax(z)=[\frac{\exp(z_1)}{\sum_c \exp(z_c)},\cdots,\frac{\exp(z_c)}{\sum_c \exp(z_c)}]^T$$

• Softmax的偏导的形式很简单，例如通过若干层的计算，最后得到的某个训练样本的向量的分数是 $[2,3,4]$ ，那么经过Softmax作用后的概率就分别为 $[0.0903,0.2447,0.665]$。如果这个样本的真实分类是第二个的话，那么偏导就等于 $[0.0903,0.2447-1,0.665]=[0.0903,-0.7553,0.665]$，然后根据偏导反向传播即可。

• 具体求偏导过程可以参考：Softmax 函数的特点和作用是什么？

BP（Backward propagation）神经网络

前馈神经网络

• 所谓前馈神经网络，就是下一层只接收上一层的信息，但是下一层永远不会给上一层传递信息。那么问题来了，前馈神经网络要怎么训练？答案是搜索。通过枚举不同的参数组合，将训练集丢进去，然后得到最终的损失函数，比较谁的损失函数最小就决定用哪组参数。

• 但是这样子的训练方式在数据量或者数据维度比较大的时候，显然是不可取的。因此，在实际的训练过程中，我们需要用到反向传播来实现参数的快速更新。

• 对于前馈神经网络，一般采用的激活函数是ReLU，但是要注意学习率的设置，不能设置过大。切忌使用Sigmoid函数，它在前馈神经网络中的表现一般不怎么好。

反馈神经网络

• 因为这一块是比较重要的内容且数学公式理解比较多，碍于篇幅问题，新开一篇文章专门研究反馈神经网络。

SGD（Stochastic gradient descent）

• 传统的GD每次训练的过程中，都需要计算所有神经元的导数。如果神经网络的结构比较庞大的话，计算这个梯度的过程也十分复杂，导致梯度更新缓慢。所以，我们引入了随机梯度下降法（SGD）。

• SGD的具体原理等和反馈神经网络一同写到上面的另一篇文章中。

---

参考链接：

CSDN-饱和和非饱和激活函数
Softmax 函数的特点和作用是什么？

课件下载链接